Low-Pass Filters Unveiled: A Comprehensive Guide to Their Function and Impact

The advancement of low-pass filters represents a significant stride in the field of electronics and audio engineering, enabling precise manipulation and enhancement of frequency responses across a myriad of applications. These filters, whether inductive, capacitive, or a sophisticated amalgamation of components, serve as serious tools in mitigating unwanted high-frequency noise while preserving required lower frequencies. The essence of low-pass filter technology lies in its ability to discriminate against frequencies, a feature that is eventual in various sectors ranging from sophisticated electronic circuitry to nuanced audio production environments.

By exploring the technical mechanics of different low-pass filters, including their construction, operational principles, and the mathematical underpinnings through transfer functions, this article explores the broad spectrum of low-pass filter applications and their profound impact on improving system performance, signal integrity, and auditory aesthetics.

Catalog

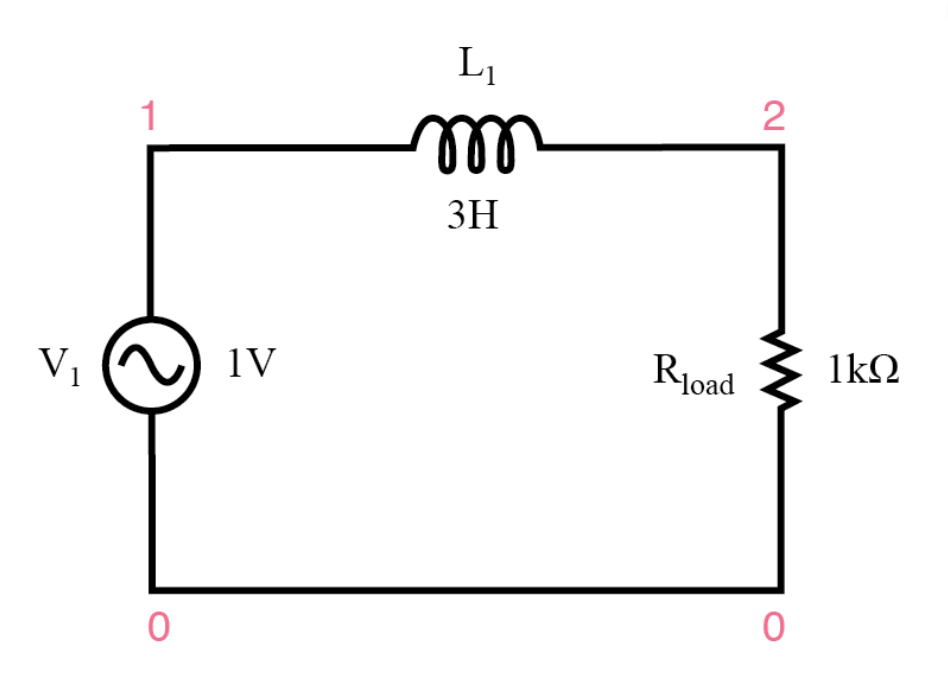
Figure 1: Inductive Low-Pass Filters

The Mechanics of Inductive Low-Pass Filters

Inductive low-pass filters are required for managing frequency distribution within circuits. They are highly effective in reducing high-frequency signals while allowing lower frequencies to pass through. The core component of these filters is an inductor, which increases its impedance as the signal frequency rises. This characteristic allows the inductor to act like a frequency-dependent resistor, increasing resistance at higher frequencies.

An inductor's impedance can be expressed as 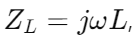, where is the angular frequency and 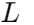is the inductance. As the angular frequency 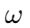rises, so does the impedance, making it better at blocking high frequencies. Conversely, at lower frequencies, the impedance remains low, allowing those signals to pass through easily.

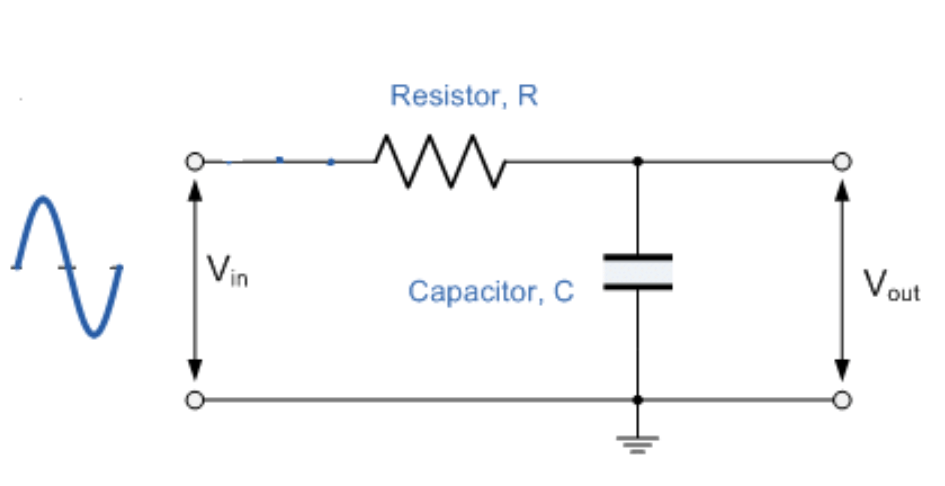
Figure 2: Capacitive Low-Pass Filters

Characteristics of Capacitive Low-Pass Filters

Capacitive low-pass filters use the unique properties of capacitors, which show decreasing impedance as signal frequency increases. By placing the capacitor in parallel with the load, these filters create a path that diverts high-frequency signals away from the output. High frequencies are then absorbed by an intermediary resistor, known as R1, which sets them apart from inductive low-pass filters.

This filter typically consists of just a capacitor and a resistor, making it simple yet highly effective. Capacitors are robust against issues like inductive coupling and energy dissipation. Unlike inductors, which suffer from resistive and magnetic losses due to their physical makeup and materials, capacitors maintain stable and predictable performance. Inductors lose efficiency because of wire resistance and magnetic hysteresis, problems that capacitors do not face, leading to a more linear and reliable response in various conditions.

Capacitive filters are especially useful in applications requiring consistent performance, such as audio equipment or signal processing devices, where signal integrity is key. While capacitive filters are widely preferred in many electronic applications, inductive filters still play a key role in specific contexts. For example, in AC-DC power supply circuits, inductive filters are needed due to their minimal series resistance, ensuring lower power loss and better efficiency despite their inefficiencies.

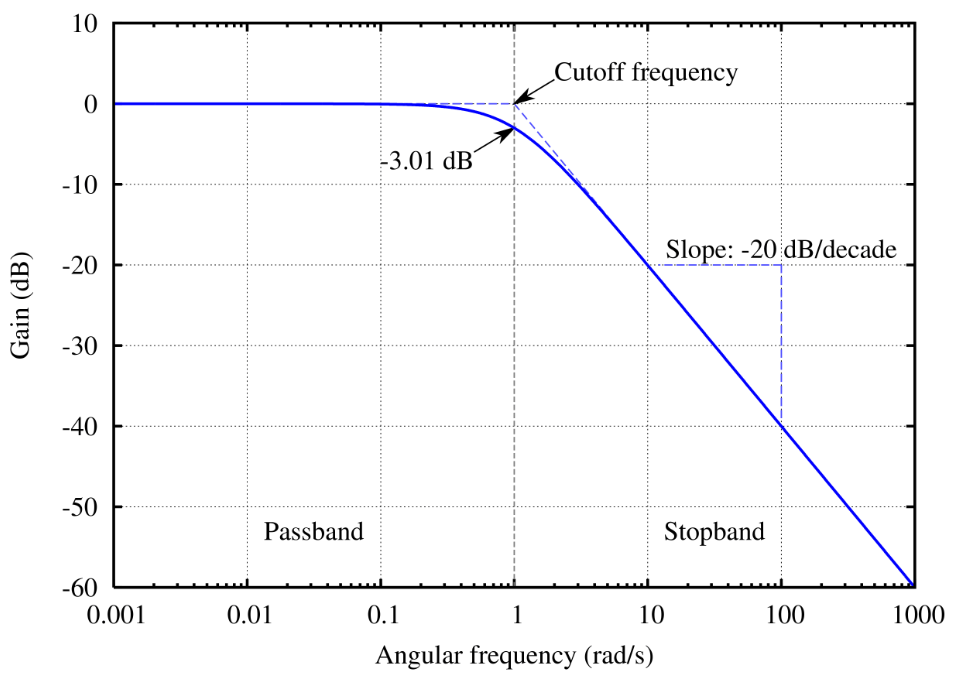
Figure 3: Cutoff Frequency

The Role of Cutoff Frequency in Electronic Filters

The cutoff frequency settles in low-pass filter design, marking the point where the filter begins to significantly reduce the input signal. Technically, it is defined as the frequency where the output voltage drops to 70.7% of its input value, corresponding to a -3 dB reduction in the logarithmic scale, which indicates halving the power. Key parameters like resistance and capacitance determine this frequency in capacitive-resistive low-pass filters.

To calculate the cutoff frequency, you set the capacitive reactance equal to the resistance. The formula is 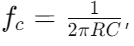, where is 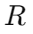resistance,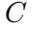is capacitance, and 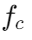is the cutoff frequency. This calculation assumes ideal conditions, but real-world performance often deviates due to factors like changes in load resistance and the non-ideal nature of components, including parasitic capacitances and inductances not considered in the initial design.

Figure 4: SPICE Simulations

To address these discrepancies, designers use SPICE simulations to model filters under realistic conditions. These simulations allow dynamic adjustment of parameters to align with desired outcomes. It's also significant to comprehend how the cutoff frequency functions in the context of a circuit. Factors like temperature and humidity can affect component characteristics, shifting the actual cutoff frequency.

Practical Applications of Low-Pass Filters

Low-pass filters are needed to enhance the performance and reliability of electronic systems, especially in environments with significant interference and noise. In power supplies for electronic devices, these filters ensure the stability and purity of the DC output by eliminating high-frequency noise. This noise can originate from various sources, such as capacitive and inductive coupling from nearby circuits, and can disrupt the device's functionality. A simple yet effective solution is to place a capacitor across the load, forming a low-pass filter that diverts high-frequency disturbances away from unsafe components. This method is particularly useful on densely populated circuit boards, where numerous electronic components are nearby, creating challenges for maintaining signal integrity.

The choice of filter—whether using capacitors, inductors, or a combination—depends on the specific needs of the circuit, including the type of noise and the sensitivity of downstream components. For example, audio electronics often require complex filter designs to preserve signal quality and ensure an undistorted output. Low-pass filters are not only used for noise reduction but also play a significant role in analog-to-digital conversion. They limit the input signal's bandwidth to the Nyquist frequency to prevent aliasing, which can degrade conversion accuracy. In wireless communications, these filters block high-frequency signals outside the desired frequency band, preventing interference and crosstalk between communication channels.

Low-pass filters are extensively used beyond traditional electronic circuits, influencing various fields from digital media to healthcare.

Refining Visual Media through Image Processing

In digital image processing, low-pass filters enhance the quality of visual media by smoothing and blurring images. This technique reduces pixel noise and high-frequency artifacts that degrade image quality. It is particularly valuable in digital photography and video production, where balancing image sharpness with noise reduction greatly affects visual appeal and clarity. In real-time applications like video streaming or augmented reality, low-pass filters help maintain high visual quality despite live data transmission challenges.

Ensuring Clarity in Telecommunication Systems

In telecommunications, low-pass filters manage signal integrity by limiting the bandwidth of transmitted signals to prevent high-frequency interference that can corrupt data and disrupt communication. Ensuring the quality of the signal across extended distances is a significant usage in both analog and digital communication systems. By using low-pass filters, errors are reduced, and the overall reliability of communication channels is enhanced.

Enhancing Diagnostic Accuracy in Biomedical Applications

In the biomedical field, low-pass filters improve the readability and reliability of physiological signal recordings, such as electroencephalograms (EEG) and electrocardiograms (ECG). These devices are sensitive to high-frequency noise that can obscure critical data, making accurate diagnosis difficult. By integrating low-pass filters, medical practitioners obtain clearer signals, improving the diagnostic process and facilitating more effective treatment plans. This application highlights the filter's importance in healthcare, where the clarity of physiological signals directly impacts patient outcomes.

Optimizing Audio Systems with Low-Pass Filters

Low-pass filters are also a versatile tool for audio engineers, allowing the manipulation of soundscapes to achieve various artistic and technical effects. Here are innovative ways these filters can be applied in audio settings:

Enhancing Spatial Depth in Mixes

Audio engineers use low-pass filters to add depth and dimension to audio tracks. By reducing higher frequencies, sounds can be made to seem more distant. This effect is especially useful in complex mixes where distinguishing between foreground and background elements enhances overall clarity and spatial perception. This technique mimics real-world auditory experiences, where distance naturally filters out higher frequencies, making sounds seem further away.

Cleaning Up Audio Tracks

In both studio and live audio environments, low-pass filters are useful for eliminating high-frequency noise or interference. Common issues like hiss, electrical hum, or overly sharp sounds from digital sources can be effectively minimized. By cutting out these unwanted frequencies, the desired audio becomes cleaner, improving the overall fidelity of the production and ensuring a polished final product.

Balancing Frequencies in Complex Mixes

Low-pass filters are key for managing frequency masking, a common challenge in dense musical arrangements where multiple sounds compete within the same frequency range. By selectively attenuating higher frequencies on certain tracks, audio engineers can prevent imperative elements from being overshadowed, maintaining a harmonious and balanced acoustic environment in the mix.

Creating Sonic Variations

Low-pass filters allow audio professionals to craft variations of the same sound within a composition, enriching the auditory landscape. This can be particularly effective in adding dynamic shifts within a track, altering the timbre and presence of sounds to suit different sections or emotional tones, thereby enhancing the musical narrative without introducing new elements.

Refining Sound Definition in Dense Mixes

In complex audio mixes, low-pass filters enhance the definition and focus of particular sounds. By reducing higher frequencies, the remaining audio becomes clearer, enabling listeners to better appreciate subtle details and intended nuances.

Optimizing Effects Buses

Low-pass filters are also needed in managing effects buses, such as reverb or delay sends. Applying these filters controls excessive high frequencies that might otherwise dominate the effects, ensuring they add to the mix without becoming intrusive. This careful control maintains the overall balance and aesthetic of the mix, allowing the effects to enhance rather than overpower the primary elements.

Clarifying Competing Sounds

Managing frequency masking, where multiple sounds compete for the same auditory space, is a common mixing challenge. Low-pass filters are invaluable here, as they attenuate the high frequencies of some tracks to prevent them from overshadowing others. This helps maintain a balanced mix where each instrument or vocal can be distinctly appreciated.

Exploring the Various Forms of Low-Pass Filters

Low-pass filter circuits are key in various electronic systems, designed to allow low-frequency signals to pass while reducing higher frequencies. The choice of filter type depends on specific application needs and desired signal characteristics, with each type offering unique advantages.

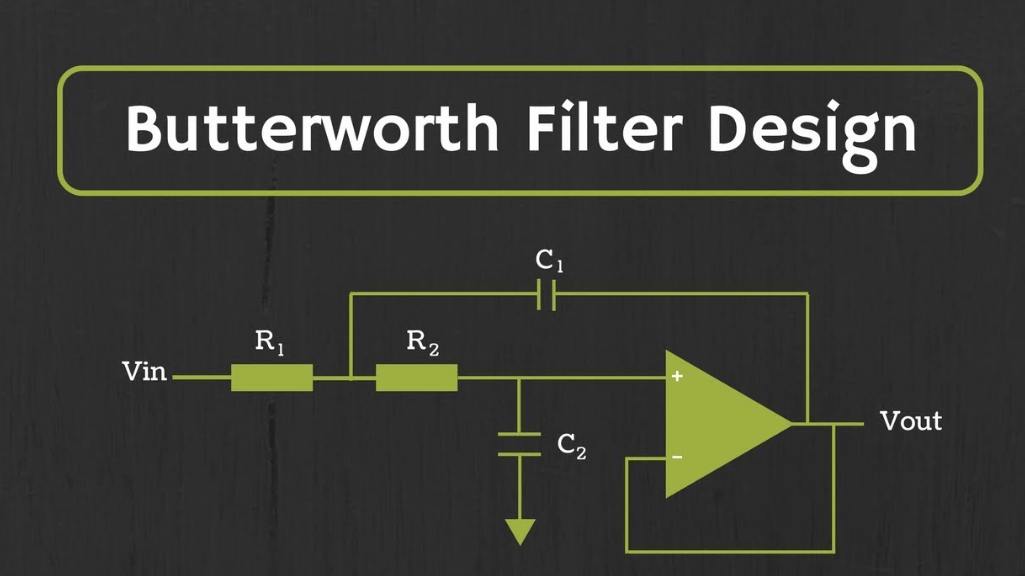
Figure 5: Butterworth Filters

Butterworth filters are known for their flat passband response, meaning they introduce no ripple in the passband. This makes them ideal for audio processing and other applications where maintaining signal integrity within the passband is a must. Their design ensures a linear response, minimizing audio signal distortion, which is significant for high-fidelity sound systems and precise measurement instruments.

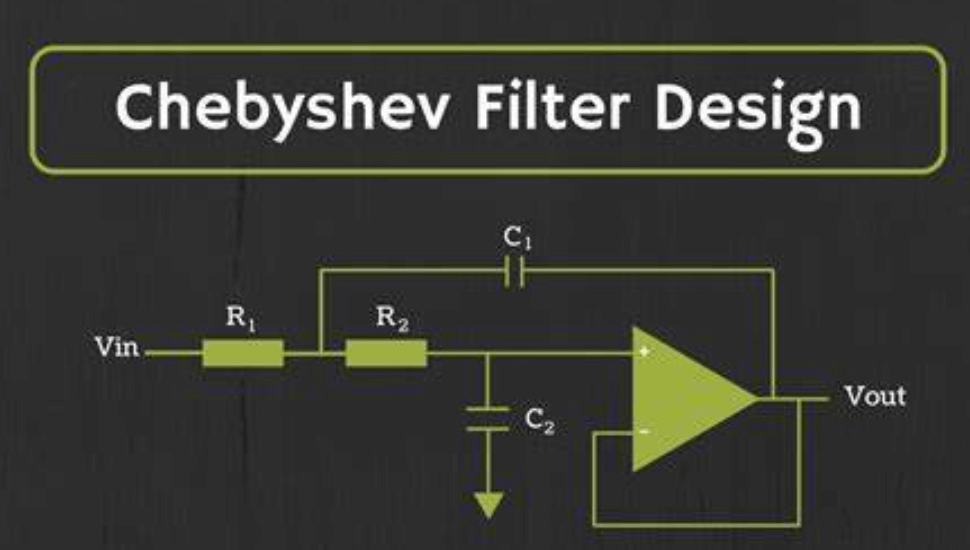
Figure 6: Chebyshev Filters

Chebyshev filters achieve a sharper roll off than Butterworth filters, providing better separation between the passband and the stopband. This is done at the cost of some ripple in the passband, a trade-off acceptable in scenarios where a steep cutoff is more unsafe. These filters are often used in communications systems, where precise bandwidth limitation is more dominant than minimal passband ripple.

Figure 7: Elliptic Filters

Elliptic filters (also known as Cauer filters) offer the steepest roll-off, allowing for a minimal transition from passband to stopband. This makes them effective in applications where space and component count are limited, such as portable and miniaturized electronic devices. The sharp transition is beneficial in densely packed frequency spectra, where minimizing adjacent channel interference is significant.

Figure 8: Bessel Filters

Bessel filters, while offering a gentler roll-off, excel in preserving the phase and shape of the input signal throughout the passband. This is dynamic in applications like pulse communications, instrumentation, and audio crossovers, where maintaining the temporal characteristics of the original signal ensures accuracy and fidelity.

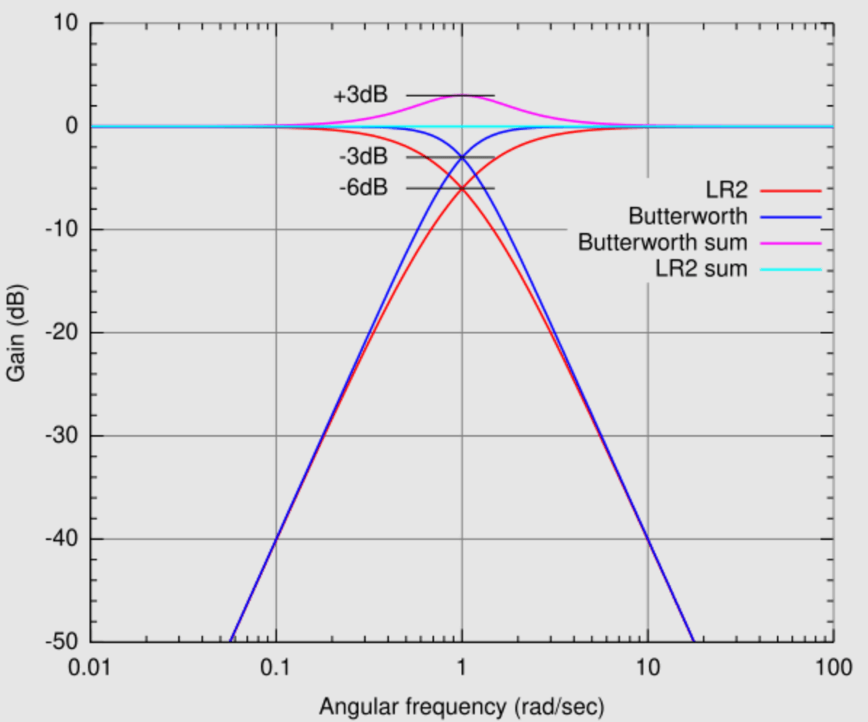
Figure 9: Linkwitz-Riley Filter

With a steep 24 dB/octave slope, this filter is the key in applications where accurate frequency division is required, such as multi-way speaker systems. In a two-way speaker setup, the Linkwitz-Riley filter divides frequencies exactly, sending high frequencies to the tweeter and low frequencies to the woofer. This ensures a smooth frequency response with minimal phase issues, which is dynamic for maintaining sound integrity in environments where audio quality is unsafe, like professional recording studios or high-fidelity sound systems.

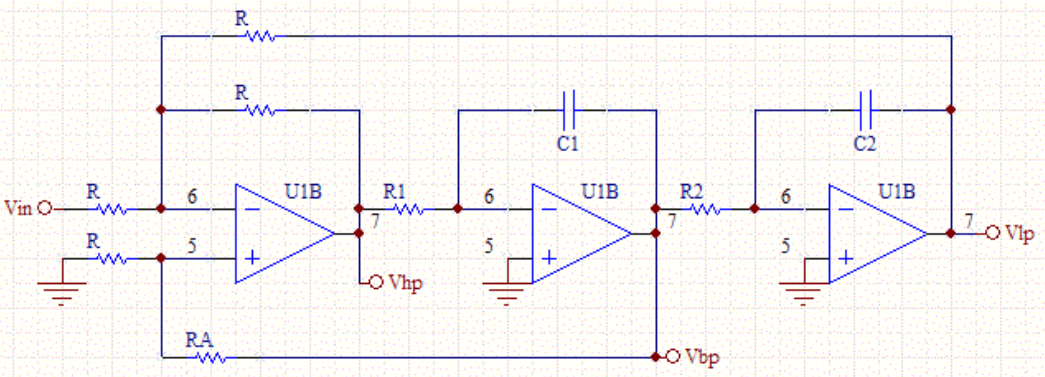
Figure 10: State Variable Filter

The State Variable Filter is notable for its versatility and usefulness in sound synthesis. Unlike traditional filters, it provides simultaneous low-pass, high-pass, and band-pass outputs. This multi-mode functionality allows for detailed control over the sound's timbral qualities in real-time, making it needed for creating electronic music. The ability to transition smoothly between different filter types helps producers craft intricate sonic textures and dynamic changes in their music. In synthesizers, this filter can modulate sounds from deep basses to crisp highs, making it requisite for sound designers.

Figure 11: Moog Filter

Known for its warm, rich sound and distinctive resonance control, it has greatly influenced various music genres, especially electronic music. The Moog low-pass filter enhances synthesizer sounds, from deep basses to smooth leads. Its resonance feature accentuates frequencies at the cutoff point, creating a peak that adds harmonic complexity. This makes the Moog filter a favorite among musicians and producers who seek to add depth, warmth, and an analog feel to their tracks, cementing its enduring legacy in music production.

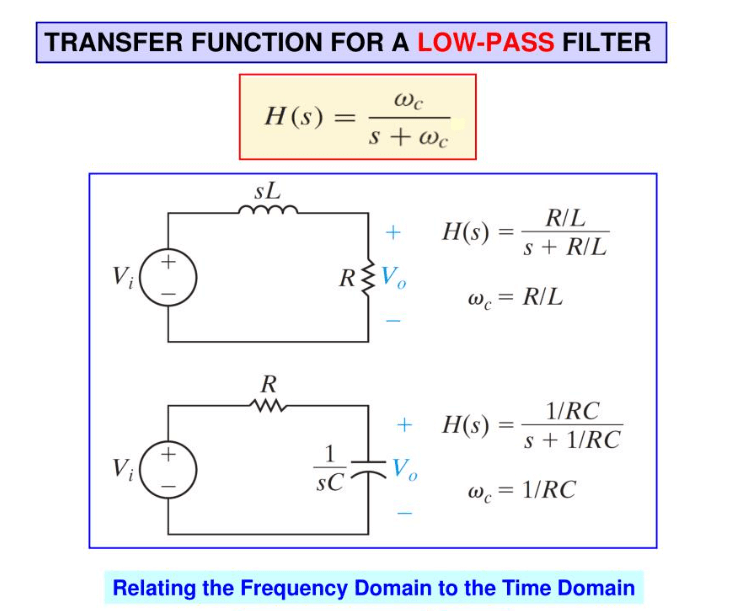
Figure 12: Transfer Function in Low-Pass Filter Design

Analyzing the Transfer Function of Low-Pass Filters

Creating efficient filtering solutions requires an extensive knowledge of a low-pass filter's transfer function. This mathematical expression shows how the amplitude and phase of an output signal vary relative to the input signal across different frequencies. The transfer function is derived from the filter's components—resistance (R), capacitance (C), and sometimes inductance (L)—and describes the filter's frequency response.

The transfer function, denoted 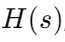 where sss is the complex frequency variable, captures the dynamics of the filter. For a simple RC low-pass filter, the transfer function is: 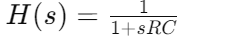This equation shows how the filter attenuates high-frequency signals while allowing low frequencies to pass with less attenuation. The RC product, known as the time constant, directly influences the cutoff frequency, the point where the filter starts to significantly attenuate higher frequencies.

In audio processing, the transfer function helps design systems that control frequency attenuation to maintain sound quality and reduce noise. In telecommunications, it enables engineers to create circuits that filter out high-frequency noise, ensuring clear signal transmission.

The transfer function is a risky tool for predicting and analyzing a filter's behavior under different conditions. By adjusting parameters within the transfer function, designers can see how changes in component values affect the filter's performance. This is particularly useful in iterative design processes, where multiple prototypes might be tested to achieve optimal results.

Mastering the Controls of Low-Pass Filters

Low-pass filters play a core role in shaping audio signals, allowing precise control over which frequencies are highlighted or reduced. This section explores the basic principles and functions of low-pass filters, underscoring their required role in audio processing.

Slope and Resonance

The slope of a low-pass filter indicates how quickly frequencies above the cut-off are reduced, affecting the filter's output. A steeper slope means a sharper drop in high frequencies, helping to isolate lower frequencies more effectively. Additionally, the resonance control can boost frequencies at the cut-off, adding a unique sound quality and enhancing specific tones. This control allows producers to add vibrancy and define the music's character.

Q Factor

The Q factor, or quality factor, measures the bandwidth around the cut-off frequency where resonance is noticeable. A high Q factor emphasizes a narrow range of frequencies, bringing more focus to that area. A low Q factor spreads the resonance over a wider range, smoothing the frequency response. This parameter is focal for audio engineers aiming to customize sounds to meet specific artistic or technical needs.

Modulation through Envelope Followers

Modulation controls, like an Envelope Follower, enhance the dynamic response of low-pass filters by varying the cut-off frequency in real time according to the input signal's amplitude. This feature allows the filter to adapt to a musical piece's dynamics, adding rhythmic and textural complexity. External modulation control expands creative possibilities in sound design, making it particularly valuable in electronic music, where dynamic textural changes can significantly influence the track's feel and progression

Conclusion

The exploration of low-pass filters across multiple domains underscores their indispensable role in contemporary technology. From refining audio mixes in music production to enhancing the reliability of electronic communication systems, low-pass filters adapt to a diverse range of challenges, ensuring optimal performance and fidelity. The detailed examination of various filter types, such as Butterworth, Chebyshev, and Moog filters, reveals their unique advantages in specific applications, highlighting the necessity for tailored filter design to meet precise operational demands.

The integration of advanced simulation tools and deep consideration of cutoff frequency dynamics further enhance the capability to predict and fine-tune filter behavior under real-world conditions. As technology progresses, the continuous evolution of low-pass filter designs will undoubtedly play a significant role in advancing electronic engineering and audio production, carving a path for innovative solutions that address both current and future challenges in signal processing.

Frequently Asked Questions [FAQ]

1. What is a high-pass and low-pass filter?

A high-pass filter allows frequencies above a certain cutoff frequency to pass through and attenuates frequencies below this cutoff. Conversely, a low-pass filter allows frequencies below a specific cutoff frequency to pass and attenuate those above it.

2. What are the advantages of a low-pass filter?

Noise Reduction: They effectively reduce high-frequency noise, making them useful in audio and electronic signal processing.

Signal Smoothing: Low-pass filters are used to smooth data by averaging rapid fluctuations, useful in data analysis and electronic circuit applications.

Stability: They help in stabilizing control systems by filtering out high-frequency oscillations.

3. What is the purpose of low-pass filters in image processing?

In image processing, a low-pass filter serves to blur images, which can reduce noise and detail. This blurring effect smooths out rapid intensity changes, which helps in image enhancement and analysis, particularly in removing small-scale details to focus on larger structures.

4. How do active low-pass filters work?

Active low-pass filters utilize active components like amplifiers, along with resistors and capacitors, to filter signals. The amplifier compensates for the signal loss due to filtering, thus maintaining the signal strength. This setup allows the filter to handle low-frequency signals effectively without significant degradation, and to be integrated easily into various electronic circuits due to its active nature.

5. What are the disadvantages of low-pass filter?

Loss of Significant Details: By attenuating high frequencies, some significant details in signals, such as sharp transitions or specific signal features, may be lost.

Phase Shift: They can introduce a phase shift in the filtered signals, which might be problematic in applications requiring precise phase alignment.

Design Complexity: Designing an effective low-pass filter that accurately balances cutoff frequency and signal integrity can be complex, especially in active filters where component choice and configuration impact performance.