Evaluating Power Factor in Electrical Circuits

In the complex field of electrical engineering, the power factor is a key indicator of AC (alternating current) circuit efficiency. Power factor, primarily, quantifies how effectively electrical power is converted into useful work output, delineating the connection between real power, which performs actual work, and apparent power, which encompasses both working and non-working components of electricity. This connection is settling as it directly influences the operational costs, energy efficiency, and reliability of electrical systems, spanning from simple residential setups to complex industrial networks.

The core of considerate and optimizing power factors lies not only in enhancing economic efficiency but also in upholding system integrity and environmental sustainability. As such, this article explores various aspects of power factor, from its theoretical underpinnings and calculation methods in different circuit types to strategic correction techniques aimed at mitigating inefficiencies and extending the longevity and capability of power systems.

Catalog

Figure 1: Power Factor Values

Measuring Power Factor Values

Power factor is an unsafe measure for evaluating the efficiency of electrical circuits. Different types of circuits affect their value in distinct ways. In purely resistive circuits, the power factor is 1.0, indicating that current and voltage are perfectly aligned with no phase difference, leading to zero reactive power. This scenario is depicted as a horizontal line in the power triangle. On the other hand, purely inductive or capacitive circuits have a power factor of zero. These circuits do not convert electrical energy into useful work; instead, they store energy temporarily in magnetic fields (inductors) or electric fields (capacitors). This creates a power triangle with a vertical line, showing that reactive power predominates and real power is absent.

Figure 2: Calculating Power Factor

The power factor measures how efficiently an electrical circuit uses power. It is the ratio of true power (P), which does productive work, to apparent power (S), which includes both real and reactive power. True power is measured in watts (W) or kilowatts (kW), while reactive power (Q), which represents unproductive power circulating in the circuit, is measured in volt-amperes reactive (VAR). The power factor can be calculated using the formula PF = cos(θ), where θ is the phase angle between the current and voltage waveforms. This angle shows how much the current leads or lags behind the voltage. The power factor varies with system characteristics and the frequency of the AC power supply, impacting the efficiency and performance of the electrical system.

For a deeper examination of power dynamics in AC circuits, several formulas are used depending on available system data. The primary formula 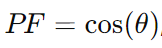directly measures the efficiency. Another formula 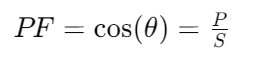shows the relationship between reactive power and apparent power, indicating how much power is not doing useful work and is contributing to the phase difference. Futhermore, 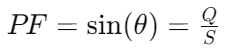correlates reactive power to true power, providing insights into how reactive power affects overall power consumption.

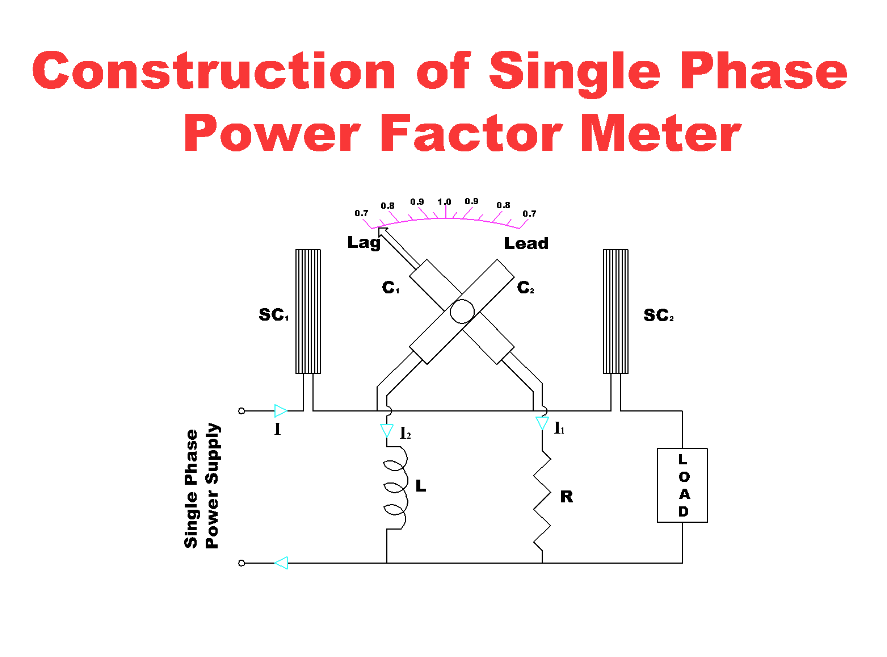
Figure 3: Power Factor in Single-Phase Circuits

Calculating Power Factor in Single-Phase Circuits

In single-phase residential electrical systems, accurate power factor measurement optimizes energy efficiency and performance.To calculate the power factor (PF), use the formula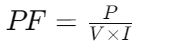 Here, P is the true power in watts (W), V is the voltage in volts (V), and I is the current in amperes (A).

Calculating Apparent and Reactive Power

To fully understand a circuit's power dynamics, first compute the apparent power using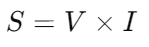 , where S is in volt-amperes (VA). Next, determine the reactive power with the formula 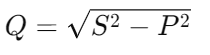, where Q is in volt-amperes reactive (VAR). These calculations show how power is distributed within the system, identifying how much power is used for useful work and how much is temporarily stored or lost.

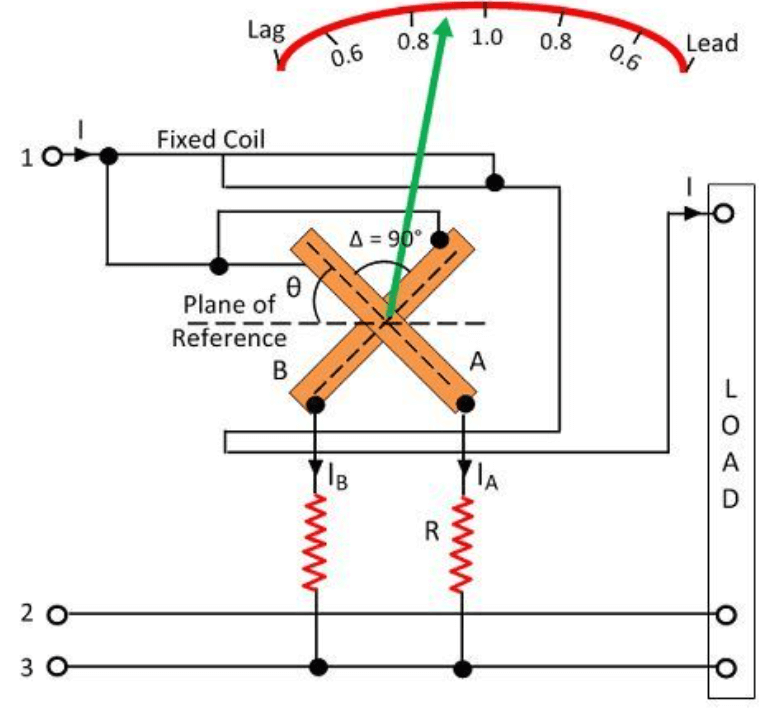
Figure 4: Power Factor in Three-Phase Circuits

Scheming Power Factor in Three-Phase Circuits

In industrial environments with three-phase circuits, accurately measuring the power factor is a must due to the complexity and power capacity of these systems. To calculate the power factor (PF), use the formula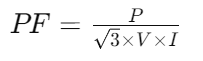 where P is the true power in watts (W), V is the voltage in volts (V), and I is the current in amperes (A). This formula takes into account the unique phase-to-phase voltage relations in three-phase systems.

For a complete power analysis, first calculate the apparent power (S) using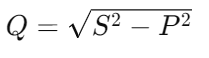 where S is in volt-amperes (VA). Then, determine the reactive power (Q) using the formula with Q measured in volt-amperes reactive (VAR).

The Importance of Maintaining a High-Power Factor

Maintaining a high-power factor is key for optimizing electrical power usage. A power factor close to 1 indicates efficient power use, while a power factor less than 1 means more current is needed to deliver the same amount of true power, signaling inefficiency. This inefficiency leads to higher energy consumption and increased operational costs.

For example, a circuit with a power factor of 0.7 requires more energy to perform tasks than a circuit with a power factor of 1. This inefficiency results in higher energy usage and costs. Improving the power factor is needed not only for cost savings but also for enhancing overall system performance and sustainability.

Efforts to improve power factor often include integrating capacitors or synchronous condensers to offset the lagging current typical in inductive loads. These measures reduce the load on the electricity supply, lower the risk of power surges and drops, and contribute to a more stable power supply.

Implications of a Poor Power Factor

Correcting a poor power factor involves strategically adding capacitors to counteract the reactive power produced by inductive loads. This approach aims to neutralize excess reactive power by generating an equal and opposite reactive force, moving the circuit’s impedance closer to a purely resistive state, which is more efficient. The process includes installing capacitors in parallel with inductive elements. This setup helps align the total impedance with pure resistance, reducing unnecessary power draw. These adjustments significantly enhance the system's energy efficiency.

Optimizing the reactive power balance not only improves efficiency but also extends the lifespan of electrical components. Efficient energy use reduces strain on power systems, minimizes heat generation, and lowers the risk of damage to sensitive equipment. By addressing poor power quality, power factor correction ensures more reliable and stable operation of electrical systems. The improved stability can lead to cost savings in the long run, as the need for maintenance and replacements diminishes.

The Impact of a Low Power Factor on Electrical Systems

A low power factor causes several negative effects on electrical systems, primarily through increased copper losses and poor voltage regulation. These problems arise because more current is needed to deliver the same amount of power, a direct result of power factor inefficiency.

Increased Current and Thermal Burden

Higher current levels increase the thermal load on the circuit's wiring. This can accelerate insulation degradation and heighten the risk of overheating. The elevated current flow also leads to greater voltage drops across the distribution network.

Effects on Device Performance and Lifespan

Voltage drops can significantly impair the performance and reduce the lifespan of electrical devices connected to the grid. Voltage instability affects device efficiency and can trigger protective relays or cause sensitive equipment to fail prematurely.

From an economic perspective, electrical utilities often charge higher rates for consumers with low power factors, reflecting the additional costs utilities incur to manage the excess current required by inefficient systems. By improving power factors, businesses can avoid these surcharges, enhance equipment reliability, and decrease overall operational expenses. Effective power factor correction strategies are significant for both industrial and commercial settings, as they help businesses avoid extra charges, improve device performance, and ensure the reliability and longevity of their electrical systems.

Common Causes of Low Power Factor

Low power factor in electrical systems can be caused by several factors, mainly harmonic currents and inductive loads.

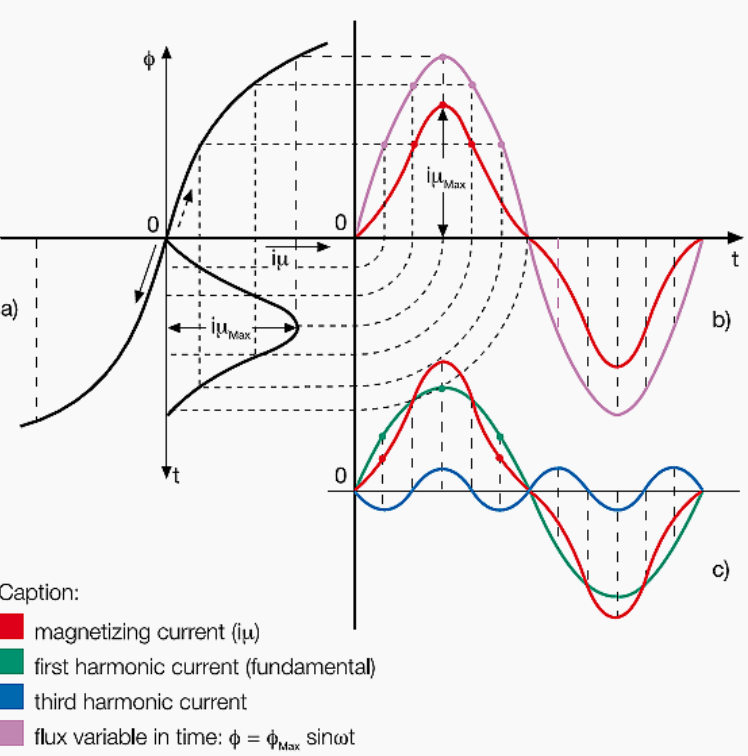
Figure 5: Harmonic Currents

Harmonic Currents, distort the sinusoidal shape of the electrical waveform. This distortion often occurs due to non-linear loads like variable-speed drives and electronic ballasts. These harmonics disrupt the efficient flow of electricity and reduce the power factor.

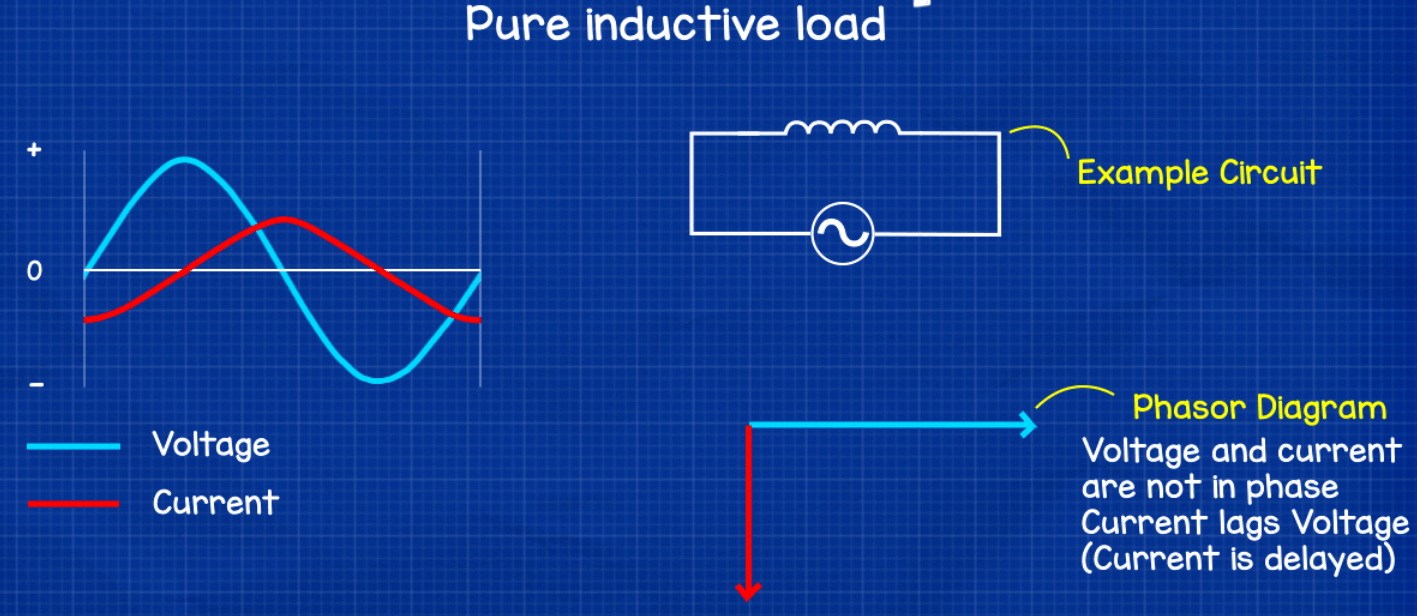
Figure 6: Inductive Loads

Inductive Loads, common in industrial settings, also lower power factor. Devices such as motors, large transformers, and induction furnaces draw reactive power, causing a phase shift between current and voltage. This phase displacement results in less effective power utilization and a decreased power factor.

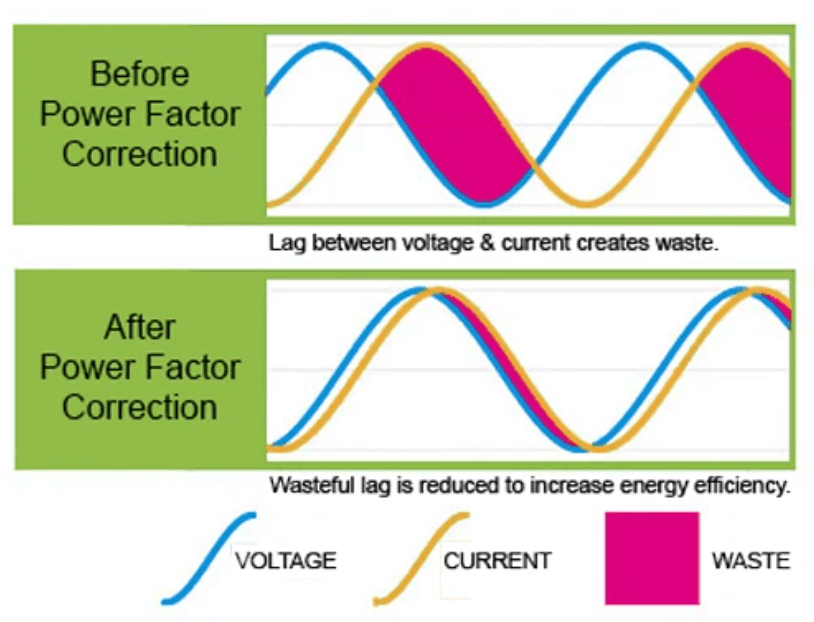
Figure 7: Power Factor Correction

Strategies for Power Factor Correction

Power factor correction involves placing capacitors or inductors in a circuit to improve the phase alignment between voltage and current, moving the power factor closer to unity. This ideal state allows for efficient energy transfer.

In circuits with inductive loads, such as motors or transformers, capacitors are used to counteract the lagging current. Capacitors provide leading reactive power, which helps balance the phase angle and improve the power factor.

In systems with capacitive loads, inductors are employed to introduce lagging reactive power. This addition balances the leading characteristics of the capacitive loads, aligning the phase angle more closely with pure resistance.

Figure 8: Electrical Loads

Origins of Poor Power Factors in Electrical Systems

Poor power factors stem from the type of load within an electrical system—resistive, inductive, or capacitive. Each load type interacts differently with the alternating current (AC) power source, affecting the system’s efficiency in using power.

• Resistive Loads: Resistive loads, like heaters and incandescent lamps, typically operate at a power factor close to 1. This is because the voltage and current are in phase, resulting in efficient power usage.

• Inductive Loads: Inductive loads, such as motors, transformers, and coils, cause a lag between the voltage and current. This lag leads to a power factor of less than 1. The energy required to establish magnetic fields around inductive components causes this delay.

• Capacitive Loads: Capacitive loads, including certain electronic circuits and capacitors, can make the current lead to the voltage. This also results in a suboptimal power factor.

Figure 9: Heavy Duty Power Factor Correction Capacitors

Enhancing Power Factor with Correction Capacitors

To improve the power factor in AC electrical systems, it needs to address inefficiencies caused by inductive loads such as motors and transformers. These loads create a phase lag between voltage and current, reducing the system's power factor. One effective method to counteract this issue is by integrating power factor correction capacitors. These capacitors introduce a leading phase angle, which neutralizes the lag caused by inductive loads. Capacitors for power factor correction come in various types, including fixed, automatic, and those engineered by manufacturers like ABB.

Capacitors work by offsetting the inductive reactance in the loads with an equivalent capacitive reactance. This improves power efficiency and reduces the burden on the electrical supply. Unlike in DC circuits where power is simply the product of voltage and current, AC circuits must consider reactance, which affects real power consumption due to the cyclical variations in current and voltage.

Figure 10: Power Factor in AC Circuits

Analyzing Power Factor in AC Circuits

The power factor in AC circuits, represented as cos(Φ), measures power usage efficiency by comparing real power (P) to apparent power (S). In an ideal, purely resistive circuit, the power factor is 1.0, meaning no phase difference between current and voltage, and real power equals apparent power. However, most practical AC circuits include inductive or capacitive components, causing phase differences that reduce power efficiency.

A high power factor indicates that most of the power is used for productive work, while a low power factor means substantial power is wasted as reactive power. Reactive power, while not contributing to actual work, is required to maintain the circuit's magnetic and electric fields.

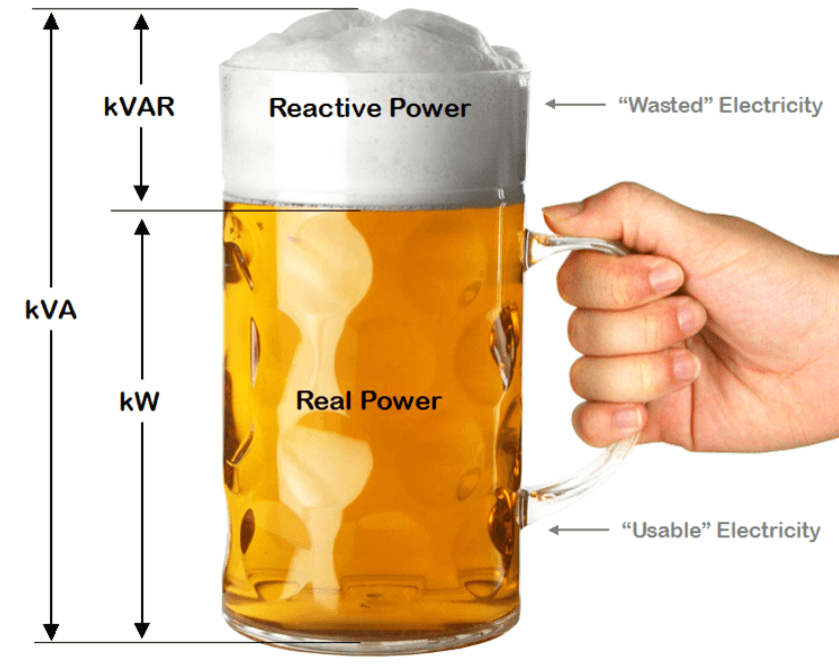
Figure 11: Power Factor Beer Mug Analogy

Power Factor Example

An analogy with a beer mug can help simplify the concept of power factors. The liquid beer represents active power, measured in kilowatts (kW), which is the effective power doing useful work. The foam on top symbolizes reactive power, measured in kilovolt-amperes reactive (kVAR), which doesn’t contribute to productive output but causes heat and mechanical vibrations. The entire mug stands for apparent power, measured in kilovolt-amperes (kVA), reflecting the total power drawn from the energy provider. Ideally, the power used by electrical circuits would match the power supplied, resulting in a power factor of one. However, inefficiencies often cause the demanded power to exceed the supplied capacity, adding strain to the utility infrastructure.

To manage these inefficiencies and maintain stability, utilities impose demand charges on large power users. These charges are based on the highest average load during a specific period, usually between 15 to 30 minutes. This strategy ensures utilities can maintain enough capacity to handle peak loads, which are serious moments when demand hits its maximum and could destabilize the power system if not managed properly. For substantial power users, the entire billing cycle’s charges are often calculated based on these peak usage times. Utilities impose surcharges on consumers with a low power factor, akin to the higher operating costs of an inefficient vehicle. Achieving a power factor of one in alternating current (AC) circuits is rare due to inherent line impedances, leading to unavoidable in.

The Downsides of a Low Power Factor

In alternating current (AC) systems, especially in three-phase circuits, the power factor is a stable parameter. The lower the power factor, the greater the current.

A low power factor increases the current flow, leading to several disadvantages. One primary consequence is higher power losses, calculated by the formula Power Loss = I² x R. For instance, a power factor of 0.8 results in power losses approximately 1.56 times greater than at a power factor of one (unity).

The use of electrical machinery like transformers and switchgear with higher kVA ratings becomes necessary due to increased power losses caused by a lower power factor, resulting in larger and more expensive equipment. This situation also leads to the need for thicker wiring to manage the higher current flow, which in turn escalates infrastructure costs.

Benefits of Optimizing Power Factor

Optimizing the power factor in electrical systems typically involves installing capacitors, using synchronous motors, or employing static VAR compensators. These measures offer several significant benefits.

Increased Efficiency and Cost Savings

Improving the power factor boosts system efficiency by reducing the reactive power component. This directly decreases the total power drawn from the utility grid, leading to lower electricity bills. A better power factor mitigates voltage drops across the system, protecting equipment from potential damage, extending its lifespan, and improving performance. It also allows for the use of smaller, more cost-effective conductors, cutting down on expenses for materials like copper.

Enhanced System Capacity and Reduced Line Losses

Managing the power factor effectively cuts line losses and reduces the size of required electrical machinery. This enhancement in system efficiency is particularly noticeable in high power factor scenarios. It not only lowers operational costs but also increases the power system's capacity to handle additional loads without the risk of overloading.

Compliance and Cost Avoidance

Aligning with utility standards is another advantage, as many service providers impose penalties for low power factors. Maintaining a high power factor can help avoid these penalties, leading to further cost savings.

Environmental Benefits

From an environmental perspective, improving the power factor reduces the energy demand needed to run electrical systems. This decrease in energy consumption lowers greenhouse gas emissions, contributing to more sustainable and environmentally friendly energy use practices.

Conclusion

Conclusively, the mastery of the power factor in electrical systems encapsulates a significant aspect of modern electrical engineering, emphasizing a meticulous balance between theoretical knowledge and practical application. By dissecting the nuances of power factors through advanced mathematical formulas and practical examples, this exploration underscores the pervasive impact of power factors on the efficiency and sustainability of electrical systems. Effective management of power factors not only minimizes operational costs and enhances equipment longevity but also contributes to environmental sustainability by reducing unnecessary energy wastage.

The strategic integration of correction devices such as capacitors and synchronous condensers, modified to specific system needs, serves as a testament to the ingenuity of power engineering. As we continue to confront the challenges posed by energy demands and environmental concerns, the role of optimized power factor remains a cornerstone in the quest for more reliable, efficient, and responsible electrical power systems. The enduring pursuit of improvement in power factors through technology and innovation reflects the broader commitment of the field to adapt and thrive in an ever-evolving energy landscape.

Frequently Asked Questions [FAQ]

1. How to calculate power factor in 3-phase?

The power factor in a three-phase system can be calculated using the formula: where PPP is the total real power in watts, VVV is the line-to-line voltage in volts, and III is the line current in amperes. This formula assumes a balanced load and does not directly take into account phase angles; for unbalanced loads, measurements for each phase must be used.

2. Why do we calculate the power factor?

Calculating the power factor is key because it helps in assessing the efficiency of the power delivery from the power source to the load. A lower power factor indicates that more current is needed to supply the same amount of power, leading to increased energy losses in the power system. Improving power factors can reduce these losses, decrease electricity costs, and relieve stress on electrical components like cables and transformers.

3. How do you measure the power factor?

Power factor can be measured using a power meter that directly displays the power factor by measuring both the real power (active power) and the apparent power (total power). These meters calculate the phase difference between the voltage and current waveforms to determine the power factor. For more precise industrial applications, specialized power factor meters are used.

4. What is the easiest way to calculate power?

For basic applications, the easiest way to calculate power (specifically, real power) is by using the formula: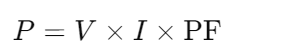 where PPP is power in watts, VVV is voltage in volts, III is current in amperes, and PFPFPF is the power factor. This straightforward method gives a quick estimation of power in circuits where voltage, current, and power factor are known.

5. What are the 3 formulas of power?

Real Power (P):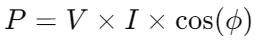 in watts, where 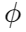is the phase angle between the current and voltage.

Apparent Power (S):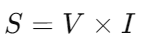 in volt-amperes, representing the total power in the circuit, combining both real and reactive power.

Reactive Power (Q):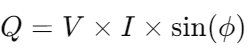  in volt-amperes reactive, which is the power stored in the field of the electrical system and returned to the source in each cycle.