Home Blog~~Detailed Guide to Full Adder~~

~~on May 10th~~ ~~625~~

Detailed Guide to Full Adder

In the realm of digital electronics and computer engineering, adders represent one of the most essential building blocks, pivotal in the construction and functionality of more intricate arithmetic circuits. As integral components of the Arithmetic Logic Unit (ALU), adders facilitate numerous computing operations, ranging from basic arithmetic to complex logical tasks necessary for system operations. Their design, which can vary from simple half-adders to more complex full adders, plays a crucial role in enhancing the efficiency and speed of processing within digital systems. This article delves into the detailed architecture and functional nuances of different types of adders, illustrating their critical role in modern computing technology and exploring their operational logic, circuitry, and applications within the broader context of digital logic design.

Catalog

1. What is an Adder?

2. Half Adder

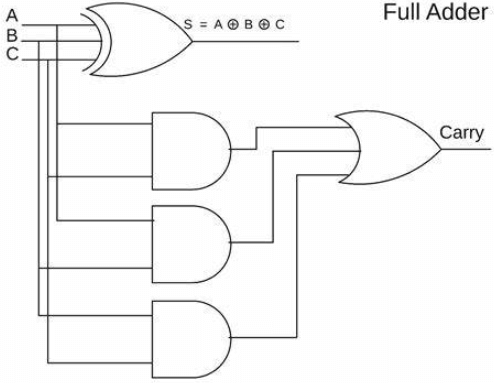
3. Full Adder

4. Full Adder Truth Table

5. Characteristics Equations of a Full Adder

6. Implementing a Full Adder Circuit

7. Advantages and Disadvantages of Full Adders

8. Applications of Full Adders in Digital Logic

9. Examples of Full Adder Implementations

10. Conclusion

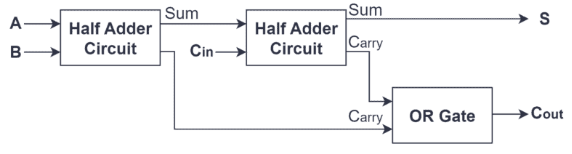
Figure 1: Full Adder

What is an Adder?

An adder is a fundamental component in electronic engineering and digital logic design and plays a central role in more complex computer systems. As a part of the Arithmetic Logic Unit (ALU), the adder handles a variety of essential computing tasks. The efficiency and performance of the entire processor are directly impacted by the design and functionality of the adder.

In the processor, the adder is used not just for basic arithmetic operations like addition and subtraction, but it also engages in a broader range of logical operations. For instance, when running programs, the processor often needs to calculate new memory addresses. This is typically done by adding to or subtracting from the current address—a task undertaken by the adder. They control the number of loop iterations and the overall flow by incrementing and decrementing counters. In more complex applications, such as table indexing, adders quickly locate data by calculating offsets. This is important for database management systems, compiler construction, and large-scale data processing. Adders are also key in implementing certain mapping techniques in multi-level cache systems, using arithmetic operations to determine the position of data in the cache, thus optimizing access efficiency.

Technologically, adders are implemented through various circuit designs including parallel, serial, and pipeline adders. Parallel adders are favored for their ability to handle multiple digits simultaneously, making them suitable for scenarios requiring fast computation. Serial adders, on the other hand, process one bit per clock cycle and are ideal for resource-limited or low-power environments. Pipeline adders divide the addition process into several stages, each handling a part of the addition operation. This design significantly boosts computation speed, especially in high-performance computing environments.

Half Adder

A half-adder circuit is a fundamental building block in digital electronics, specifically designed to add two single binary digits. This circuit forms the foundation of a full adder and is key to understanding more complex logic circuit designs. In a half adder, there are two primary inputs, labeled A and B, which represent the augend and the addend respectively. This setup enables it to compute the sum and carry output without the need for a carry input from previous calculations.

The core of a half-adder consists of two logic gates: an XOR gate and an AND gate. The XOR gate is responsible for generating the sum output. It operates under a simple rule where it outputs a 1 if only one of its inputs is 1; otherwise, it outputs a 0. The AND gate, on the other hand, handles the carry output. It produces a 1 only when both its inputs are 1, aligning perfectly with the fundamental requirements of binary addition.

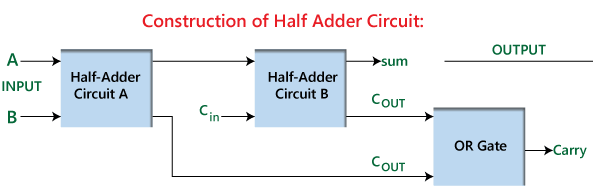
Figure 2: Construction of Half Adder

This efficient and straightforward design allows the half adder not only to perform basic binary addition independently but also to serve as a building block for creating a full adder. A full adder is constructed by combining two half adders with an additional OR gate. In this setup, the first half adder takes on the initial addition task, generating a preliminary sum and carry. The second half adder then processes the carry from the first along with an additional carry input. Finally, the OR gate merges the two carry outputs to produce the final carry output. This arrangement enhances the functionality of the adder, enabling it to handle more complex multi-bit addition tasks, showcasing the widespread application and importance of half adders in digital circuit design.

Full Adder

A full adder is an advanced component in digital logic design, equipped to handle the addition of three single-bit binary inputs, commonly labeled as A, B, and carry-in (Cin). This design allows the full adder to efficiently process complex binary additions by incorporating the carry from previous lower-order calculations into a single operation.

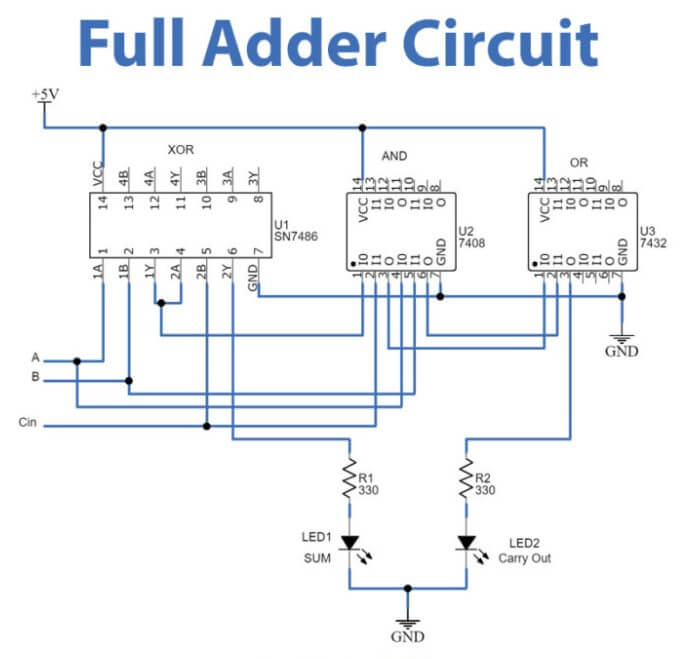
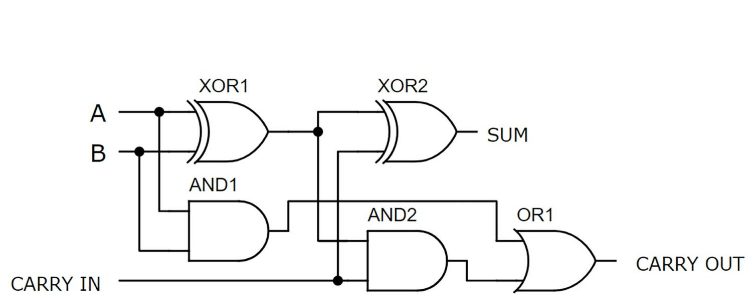
Figure 3: Full Adder Circuit

Functionally, a full adder can output a two-digit sum, which means its output can range from 0 to 3, and it can also produce a carry-out (Cout). This happens because, when all input bits are set to 1 (A=1, B=1, Cin=1), the sum output will be 1 (representing binary 01), and a carry-out of 1 is generated, indicating that an additional carry needs to be passed to the next higher bit.

Structurally, the full adder generally consists of two half adders and one OR gate. The first-half adder takes inputs A and B, generating an initial sum and a carry signal. This initial sum is then fed, along with the carry-in (Cin), into the second half-adder. The second half adder's role is to add this sum from the first half adder to Cin, producing another sum and a new carry output. Simultaneously, the carry output from the first half adder and the carry output from the second half adder are merged through an OR gate, culminating in the final carry-out (Cout) of the full adder. The design of this structure ensures that the full adder effectively handles the propagation of carriers in addition operations, making it ideal for executing multi-bit binary additions. Thus, the design of the full adder not only speeds up data processing and enhances efficiency but also simplifies the complexity of hardware implementation through a straightforward combination of logic gates, making it an indispensable component in multi-digit addition and the Arithmetic Logic Unit (ALU).

Parameters	Half Adder	Full Adder
Description	Half Adder is a combinational logic circuit that adds two 1-bit digits. The half-adder produces a sum of the two inputs.	A full adder is a combinational logic circuit that performs an addition operation on three one-bit binary numbers. The full adder produces a sum of the three inputs and carry value.
Previous carry	The previous carry is not used.	The previous carry is used.
Inputs	In Half adder, there are two input bits (A, B).	In full adder, there are three input bits (A, B, C_in).
Outputs	The generated output is of two bits-Sum and Carry from the input of 2 bits.	The generated output is of two bits-Sum and Carry from the input of 3 bits.
Used as	A half-adder circuit cannot be used in the same way as a full-adder circuit.	A full adder circuit can be used in place of a half adder circuit.
Feature	It is simple and easy to implement	The design of a full adder is not as simple as a half adder.
Logical Expression	Logical Expression for half adder is: S=a⊕b; C=a*b.	Logical Expression for Full adder is: S=a⊕b⊕Cin; C_out=(ab)+(C_in(a⊕b)).
Logic gates	It consists of one EX-OR gate and one AND gate.	It consists of two EX-OR, two AND gates, and one OR gate.
Applications	It is used in Calculators, computers, digital measuring devices, etc.	It is used in Multiple bit additions, digital processors, etc.
Alternate name	There is no alternate name for half adder.	A Full adder is also known as a ripple-carry adder.

Chart 1: Difference between the Half Adder and Full Adder

Full Adder Truth Table

The truth table of a full adder is the key to understanding its operational logic, detailing the precise relationship between binary input combinations and their corresponding outputs. This table demonstrates all potential input scenarios and their outcomes, making it an essential tool in the design and verification of digital logic circuits. The full adder processes three inputs: A, B, and a carry-in (Cin), each of which can be either 0 or 1. This results in eight possible combinations of inputs.

For each of these combinations, the outputs from the full adder include a sum (Sum) and a carry-out (Cout). The sum is the modulo-2 addition (XOR operation) of the three inputs—A, B, and Cin. The carry-out occurs when at least two of the input bits are 1. This reflects the full adder's capability to handle the carry-over in sequential addition operations, ensuring accuracy in higher-bit calculations.

To illustrate, consider the input scenario where all inputs are 0 (A=0, B=0, C-in=0). The output sum will be 0, and the carry will also be 0, indicating that there is no additional sum or carry to manage. If only one input bit is 1, such as A=1, B=0, C-in=0, the output sum will be 1 with no carry, showing that there is no need to transfer a carry to a higher bit. When two input bits are 1, like A=1, B=1, C-in=0, the output sum is 0 (since 1+1 equals 2 in binary, and modulo-2 results in 0), but the carry-out is 1, indicating a carry that needs to be passed to the next higher bit. The most complex scenario occurs when all three input bits are 1 (A=1, B=1, C-in=1); the output sum is 1, and there is a carry-out of 1, suggesting that carry management may also be required at even higher bits.

A	B	C_in	S	C_out
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Chart 2: Full Adder Truth Table

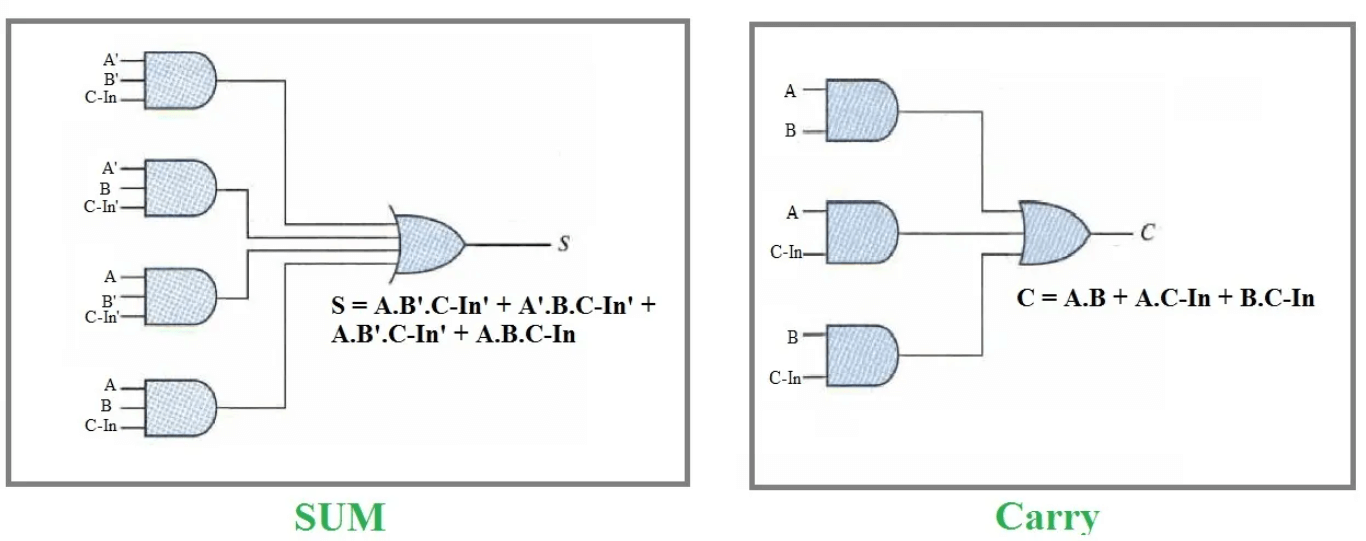
Characteristics Equations of a Full Adder

Understanding the full adder involves dissecting its functionality using the truth table, where different combinations of input values A, B, and C-IN lead to outputs SUM and COUT. To grasp the operation, we simplify the logic equations step by step.

Logic Expression for SUM

The equation starts with the distinct cases where the sum equals 1:

• A' B' CIN + A' B CIN' + A B' CIN' + AB CIN

This equation can be condensed by grouping terms with and without CIN:

• CIN (A' B' + AB) + CIN' (A' B + A B')

This simplification leads to an easier-to-implement form:

• CIN XOR (A XOR B)

This representation shows that the sum output is essentially the XOR operation among A, B, and CIN, capturing the core behavior of binary addition where SUM toggles based on an odd number of ones.

Logic for COUT

Starting with conditions where the carry is generated:

• A' B CIN + A B' CIN + AB C-IN' + AB CIN

Simplifying the equation, we identify terms that commonly involve generating a carry:

• AB + B CIN + A CIN

Looking for another method to implement COUT, the equation can be re-organized:

• AB + A CIN + B C-IN (A + A')

This expands and recombines to capture all scenarios where at least two inputs are 1:

• AB CIN + AB + A C-IN + A' B CIN

• AB (1 + CIN) + A C-IN + A' B CIN

• AB + A C-IN (B + B') + A' B CIN

• AB + A B' CIN + A' B CIN

• AB + CIN (A' B + A B')

The final compact form for COUT:

• AB + CIN (A XOR B)

This version of the carry-out equation demonstrates how COUT is produced either when both A and B are 1, or when one of A or B is 1 along with a carry-in, thus encapsulating the logic needed to manage carry propagation in multi-bit binary addition. This streamlined logic is particularly useful for implementing efficient digital circuits.

Figure 4: Equations of a Full Adder

Implementing a Full Adder Circuit

Implementing a full adder circuit involves carefully assembling two half adders and an OR gate to create a device capable of efficiently handling the addition of three single-bit binary inputs. This arrangement optimizes the circuit’s complexity and ensures both efficient and accurate computations.

To start, the first half adder takes two primary binary inputs, A and B, which are the main digits to be added. Its key task is to compute the sum and the initial carry of these two numbers. Here, the first half adder delivers two outcomes: an initial sum (Sum1) and an initial carry (Carry1). Sum1 is derived from the XOR operation of A and B, indicating whether the total has an odd number of 1's. Carry1, the result of the AND operation between A and B, indicates whether both digits are 1, necessitating a carry to the next higher bit.

Next, the second half adder joins the process. It uses the sum output Sum1 and the third input Cin (carry-in from a previous calculation) as its inputs. The second half adder produces two outputs: the final sum result (Sum2) and the secondary carry (Carry2). Sum2, which is the XOR result of Sum1 and Cin, represents the final sum of the three inputs, displaying the aggregated binary addition. Carry2, emerging from the AND operation between Sum1 and Cin, indicates a carry generated by these components.

Figure 5: Full Adder Circuit with Using Two Half Adder

Finally, to complete the full adder’s design, an OR gate is required to handle the carry outputs Carry1 and Carry2 from both half adders. This OR gate ensures that any carry generated during the computations is correctly forwarded to the final output. Therefore, the full adder’s final carry output (Cout) is the OR result of Carry1 and Carry2. The inclusion of this OR gate guarantees that all potential carries are accurately calculated and conveyed to the next level in multi-bit addition operations, ensuring the integrity of the arithmetic operation across multiple bits.

Advantages and Challenges of Full Adders in Digital Logic

Full adders play an indispensable role in digital logic design, offering numerous benefits that make them essential in various computing and data processing scenarios. Their primary advantages include remarkable flexibility, swift processing speeds, and efficient carry management. These traits make full adders ideal for executing complex arithmetic operations and logic functions, particularly in applications requiring sequential multi-bit addition.

Advantages

Flexibility: Full adders excel in their ability to process multiple binary inputs (A, B, and Cin) simultaneously. They can also be expanded into larger adder arrays to handle longer binary numbers. This scalability is important for building high-performance Arithmetic Logic Units (ALUs), which must carry out intricate multi-bit arithmetic and logic operations.

Speed: Thanks to their internal parallel processing architecture, full adders can complete the addition of all inputs in a single clock cycle while also determining to carry outputs. This capability supports continuous addition operations and is indispensable for real-time data processing in modern microprocessors and high-speed computing devices.

Disadvantages

However, full adders also present notable disadvantages:

Complexity in Design and Implementation: Full adders involve multiple logic gates and multi-level carry propagation, making their design complex. This complexity not only increases manufacturing costs but can also impact the reliability of the circuits.

Propagation Delay Issues: Carry propagation may pass through several logic gates, each adding its delay. This can limit the overall computational speed during large-scale operations, particularly in extensive computer systems and in the design of Very-Large-Scale Integration (VLSI) and high-speed processors. The delay can become a significant bottleneck in performance.

To mitigate these issues, engineers continuously explore more efficient circuit designs. Strategies include using faster logic gate technologies, optimizing circuit layouts to shorten path lengths, and developing advanced technologies like carry-save adders to minimize delays in carry propagation.

Applications of Full Adders in Digital Logic

Full adders are extensively used in digital logic, prized for their flexibility and efficiency, making them central to a multitude of computing and data processing tasks. Their application spans from basic arithmetic operations to complex signal processing and system control. Here’s a detailed look at some key areas where full adders are integral.

Arithmetic Circuits

One of the most straightforward uses of full adders is in arithmetic circuits where they perform binary addition. Especially crucial in multi-bit number addition, full adders manage longer binary sequences through cascading. In this arrangement, each full adder handles the addition for its bit position and the carry from the lower bit, then passes the new carry to the next higher bit's full adder. This cascade enables comprehensive multi-bit addition across the entire range of digits.

Data Processing

Full adders also play a pivotal role in advanced data processing tasks such as digital signal processing (DSP) for filtering and Fourier transforms, where precise and fast arithmetic operations are needed. Additionally, in the realm of information security, including data encryption and error detection and correction algorithms like parity checks and cyclic redundancy check (CRC) code generation, full adders are crucial for executing essential bit operations.

Counters

In digital counters, full adders are indispensable for implementing both increment and decrement functions, particularly in modular and synchronous counters. They accurately manage carries and borrows to ensure precise counting.

Multiplexers (MUX) and Demultiplexers (DEMUX)

In multiplexers and demultiplexers, full adders play a critical role in channel selection and data distribution. They participate in the logic that determines which channels are used for data input and output, making decisions based on logic control signals.

Memory Technology

In memory addressing, full adders help generate address signals for dynamically accessing memory locations. This is particularly important in dynamic random-access memory (DRAM) and other storage systems, where full adders support complex address calculations to enhance the efficiency of memory access.

Arithmetic Logic Units (ALU)

Finally, as fundamental components of Arithmetic Logic Units in microprocessors and digital signal processors, full adders are crucial. The ALU handles all arithmetic and logic operations, with full adders ensuring data is processed both swiftly and accurately.

Examples of Full Adder Implementations

Full adders can be constructed using various logic gates and configurations. Here, we explore four different implementations, highlighting their setup and operational nuances.

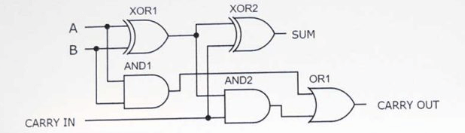
Full Adder Built with XOR, AND, and OR Gates

Figure 6: Full Adder Built with XOR, AND, and OR Logic Gates

This example showcases a full adder built on a breadboard using discrete transistors. The configuration comprises five logic gates: two XOR gates, two AND gates, and one OR gate, requiring a total of 21 transistors. Inputs A and B are connected to the breadboard’s top left, receiving a +5V supply. These inputs are controlled using two toggle switches. Two LEDs at the top left indicate the states of inputs A and B, while two LEDs on the right side display the outputs. The resistors used in the circuit are all 2.2K ohms. When inputs A and B are on and the carry-in is off, the output shows a binary value of 10, representing the sum 2 (1 + 1 + 0 = 10). The XOR gates, built with the first 12 transistors, handle the primary summation, while the lower half of the breadboard contains the AND and OR gates for carry operations, color-coded wiring enhances clarity and troubleshooting.

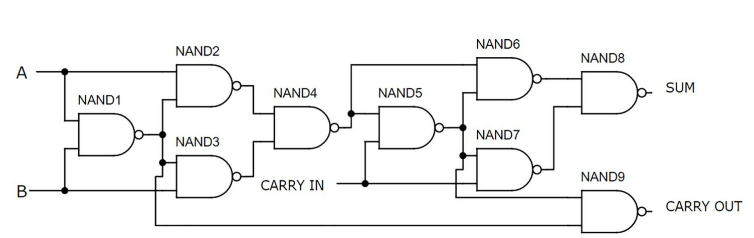
Full Adder Using NAND Gates

Figure 7: Full Adder Using NAND Gates

This full adder utilizes nine NAND gates, with each gate made from two transistors, totaling 18 transistors. This method is among the simplest and most efficient ways to construct a full adder using discrete components. All the gates are assembled on the upper half of the breadboard, while switches occupy the lower half. The circuit's functionality is demonstrated with inputs A and B on and the carry-in off, resulting in an output binary value of 10, equivalent to the decimal 2.

Full Adder with NOR Gates

Figure 8: Full Adder with NOR Gates

Constructed with nine NOR gates, each requiring two transistors, this setup also uses 18 transistors in total. Building a full adder with NOR gates offers a good alternative but involves more complex wiring compared to NAND gates. Each transistor in the NOR gates is grounded, with the collectors connected by orange jumper wires to ensure neat and organized wiring. This configuration is shown with inputs A and B activated and the carry-in deactivated, leading to the outputs where the carry is active and the sum is off.

Conclusion

Throughout this exploration of adder technology, from basic half adders to sophisticated full adder designs, it is evident that these components are foundational to the advancement of digital electronics. The operational characteristics and implementation examples provided underscore the versatility and efficiency of adders in various computational settings. By examining the structure and function of adders, particularly through their truth tables and characteristic equations, we gain valuable insights into their capabilities and constraints. This knowledge is instrumental in advancing the design of more efficient and faster computing systems. Ultimately, adders not only simplify complex binary calculations but also enable the proliferation of technology in areas as diverse as data processing, memory allocation, and digital signal processing. As digital technology evolves, the ongoing refinement and innovation in adder design will continue to be a cornerstone in the development of more advanced computational architectures, ensuring that these fundamental components remain at the heart of digital system design and implementation.

Frequently Asked Questions [FAQ]

1. What is a full adder circuit?

A full adder is a digital circuit that adds three binary bits to produce a sum and a carry output. It is designed to handle the addition of three inputs: two significant bits and one carry-in bit from a previous addition. This allows it to be used in successive stages to add multi-bit binary numbers.

2. How many AND, OR, XOR in full adder?

A typical full adder contains:

Two XOR gates for generating the sum.

Two AND gates to contribute to the carry-out calculation.

One OR gate to finalize the carry-out output.

3. What is carry input in full adder?

The carry input (Cin) in a full adder is the carry bit from the addition of the previous lower significant bits in multi-bit binary addition. It allows the full adder to consider this previous carry when calculating the current sum and the new carry-out.

4. Why use a full adder instead of a half adder?

A full adder is used instead of a half adder because it can add three bits (including the carry from previous additions), making it suitable for chaining together to add multi-bit numbers. A half-adder can only add two bits and does not have a provision for a carry-in, which limits its use to the simplest forms of binary addition without sequential carry propagation.

About us

ALLELCO LIMITED

Allelco is an internationally famous one-stop procurement service distributor of hybrid electronic components, committed to providing comprehensive component procurement and supply chain services for the global electronic manufacturing and distribution industries, including global top 500 OEM factories and independent brokers.
Read more